Unidad IV: La Circunferencia

 

Circunferecia y Círculo. Definición y Elementos

 Una circunferencia es una línea curva y plana cuyos puntos están todos a la misma distancia de otro punto llamado centro.
  Un círculo es la región del plano limitada por una circunferencia.

 

Elementos en la Circunferencia

 

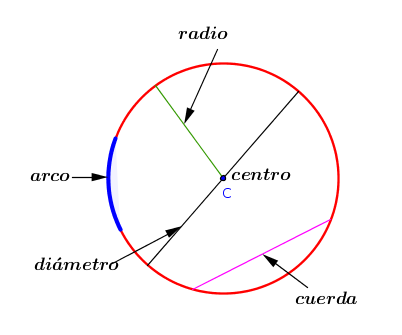
 Centro (C): Punto interior que equidista (está a la misma distancia) de todos los puntos de la circunferencia.
 Radio : Segmento que une el centro con cualquier punto de la circunferencia.
 Diámetro : Segmento que une dos puntos de la circunferencia y pasa por el centro.
La longitud del diámetro es dos veces la del radio (d = 2r).
 Cuerda : Segmento que une dos puntos de la circunferencia.
 Arco: Trozo de circunferencia delimitado por dos puntos de la misma.

Regiones Circulares

 

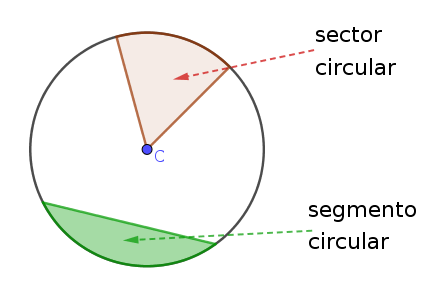
 Sector Circular: región de círculo comprendida entre dos radios
 Segmento Circular: región de círculo comprendida entre una cuerda y su arco

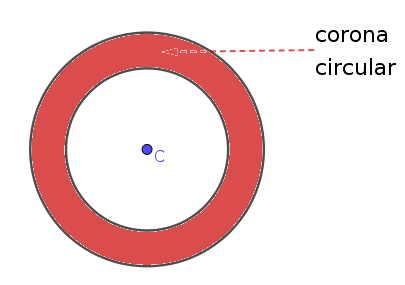
Corona Circular: región de círculo comprendida entre dos círculos concéntricos (con el mismo centro)
 

 

 
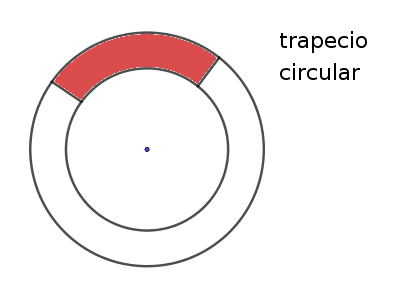
 Trapecio Circular: región de corona circular delimitada por un ángulo central

 

 POSICIÓN RELATIVA DE DOS CIRCUNFERENCIAS

La posición relativa entre dos circunferencias viene determinada por la distancia entre sus centros (d) y el valor de sus radios R y R'. 

Se tienen los casos siguientes: 

Exteriores: La distancia entre los centros, d, es mayor que la suma de los radios. Las circunferencias no tienen puntos en común

 

Secantes: La distancia d es menor que la suma de los radios y mayor que su diferencia. Tienen dos puntos en común.

 

Interiores: La distancia entre los centros es mayor que cero y menor que la diferencia entre los radios. Una circunferencia está dentro de la otra, y por tanto no tienen puntos en común.

 

Tangentes Exteriores: La distancia entre los centros es igual a la suma de los radios. El centro de cada circunferencia es exterior a la otra y tienen un punto en común, punto de tangencia

 

Tangentes Interiores: La distancia entre los centros es igual a la diferencia entre los radios. El centro de una de las circunferencias está dentro de la otra. Tienen un punto en común.

 

Concéntricas: Tienen el mismo centro. La distancia d=0. No tienen puntos en común, salvo que R=R', en este caso son la misma circunferencia.

 

Haga CLick Aquí para ver un video sopre la posición relativa de dos circunferencias 

Angulos En la Circunferencia

 Angulo Central: Es aquel ángulo cuyo vértice esta en el centro de la circunferencia y sus dos segmentos que lo forman son radios. Una de las características más importantes de este ángulo es que tiene la misma medida que el arco que lo subtiende.

Angulo Inscrito:  Es aquel cuyo vértice está en la circunferencia sus ramas están también en el circunferencia y permite mantener la medida del ángulo fija. Una de sus características principales es que el arco que lo subtiende mide el doble de su medida

Ángulo Semi-Inscrito: Ángulo semi-inscrito es aquel que tiene el vértice en la circunferencia, y sus lados son  una cuerda y una tangente a la circunferencia. La medida del ángulo semi-inscrito es igual al ángulo inscrito cuyo arco sostiene.

 

Ángulo Interno: Es aquel que tiene su vértice dentro de la circunferencia,  pero en un punto diferente al centro. Se forma por la intersección de dos cuerdas.

 

Su medida equivale  a la "semi-suma"  de los dos arcos que subtienden al ángulo interno.  

Ángulo Exterior: Es aquel formado por dos secantes que se intersectan en un punto exterior a la circunferencia. Su medida corresponde a la mitad de la diferencia entre los arcos que subtienden a este arco.

 

 

 
CUADRILÁTEROS INSCRIPTIBLES Y CIRCUNCRIPTIBLES.

En un triángulo, siempre es posible trazar una circunferencia que pase por sus vértices, (circunferencia circunscrita) y otra tangente a sus lados (circunferencia inscrita), pero en un cuadrilátero, en general esto no es posible, si en algunos casos particulares.

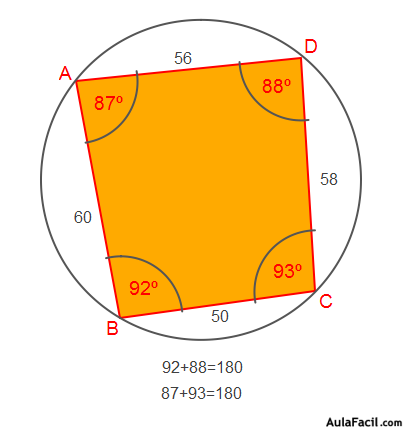
CUADRILÁTEROS INSCRIPTIBLES: Se denominan también cuadriláteros cíclicos, es  un cuadrilátero cuyos vértices son puntos de una circunferencia, si es se cumple se dice que está inscrito en ella. Tambien un cuadrilátero es inscriptible , si sus ángulos opuestos son suplementarios. 

 

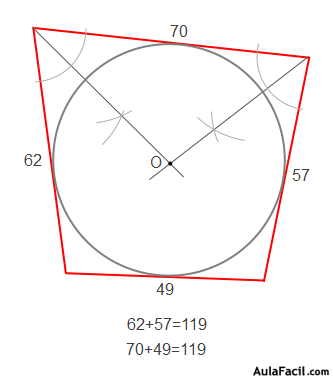
CUADRILÁTEROS CIRCUNSCRIPTIBLES. Es un cuadrilátero cuyos lados son tangentes a una misma circunferencia. (Equivalentemente, es un cuadrilátero en el que es posible inscribir una circunferencia.). Un cuadrilátero es circunscriptible si la suma de dos lados opuestos es igual a la suma de los otros dos.

 

Propiedades de las Tangentes en la Circunferencia 

TANGENCIAS

La palabra tangente proviene del latín “tangens” que significa “que toca”, esto es, que tiene un punto en común sin cortarse.

PROPIEDAD 1

Si dos circunferencias son tangentes, el punto de tangencia está el la recta O1O2.

PROPIEDAD 2

Si una recta es tangente a una circunferencia, el punto de tangencia está en la perpendicular a r trazada por O.

 

PROPIEDAD 3

Si una circunferencia pasa por dos puntos, su centro está en la mediatriz del segmento que une dichos puntos.

 

PROPIEDAD 4

Si una circunferencia es tangente a dos rectas su centro está en la bisectriz del ángulo que forman dichas rectas.

 

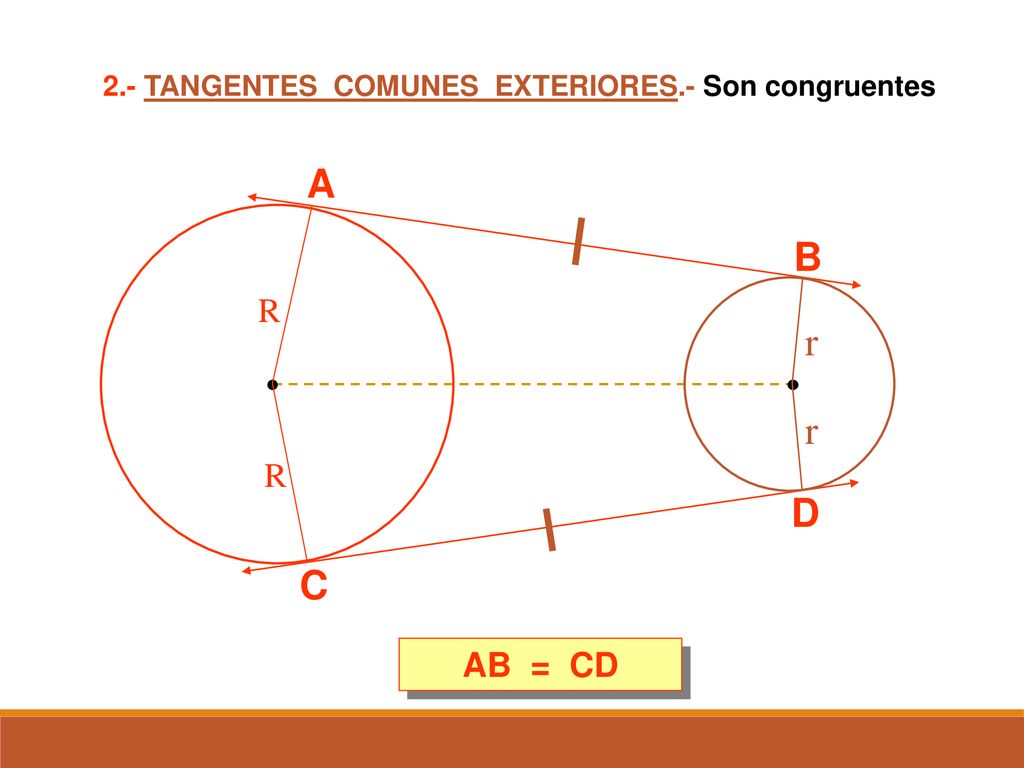
Tangente Interiores o Exteriores: En dos circunferencias exteriores  se cumple  que las tangentes exteriores o interiores son congruentes.

Propiedad de la Secante y una Tangente: Si un segmento tangente y un segmento secante se dibujan hacia un círculo desde un punto exterior, entonces el cuadrado de la medida del segmento tangente es igual al producto de las medidas del segmento secante y su segmento secante externo. 

 

En el círculo, es una tangente y es una secante. Estas se intersectan en el punto U .

Así, . 

Ejemplo :

En el círculo mostrado, si UX = 8 y XY = 10, entonces encuentre la longitud de UV .

Sustituya.

Realice la raíz cuadrada en cada lado.

 

LÍNEAS PROPORCIONALES EN EL CÍRCULO

Se presentan tres propiedades o teoremas:

TEOREMA 1:

Si dos cuerdas se cortan dentro de un círculo, el producto de los dos segmentos de una, es igual al producto de los dos segmentos de la otra.

  

Nota: el punto E está ubicado en la intersección de la dos cuerdas

 TEOREMA 2:

Si desde un punto exterior a un círculo, se traza dos o más secantes, el producto de una de ellas y su parte externa es igual al producto de la otra y su parte externa.

 

En los siguientes videos verás la demostración de estas propiedades:

1. Click Aquí para ver el video 1: 
2. Click Aquí para ver el video 2:
3. Click Aquí para ver el video 3:
4. Click Aquí para ver el video 4:
5. Click Aquí para ver el video 5:

Resuelva los Siguientes Ejercicios:

 

 

 

 

 

 

 

 

 

 

.