Homotecia

Isometría y Transformaciones Isométricas 

La palabra isometría proviene del griego iso (prefijo que significa igual o mismo ) y metria (que significa medir ). Por ello, una definición adecuada para isometría sería igual medida.

 

Cuadrado simétrico, una construcción isométrica. 

Se denomina transformación isométrica de una figura en el plano aquella transformación  que no altera ni la forma ni el tamaño de la figura en cuestión y que solo involucra un cambio de posición de ella (en la orientación o en el sentido), resultando que la figura inicial y la final son semejantes , y geométricamente congruentes .

Además de relacionarse con la semejanza y la congruencia en las figuras planas, las transformaciones isométricas tienen una estrecha relación con la expresión artística, apoyada en la construcción geométrica (por ejemplo, en las teselaciones ).

Por ello, en el aula, el tópico isometría se puede desarrollar en torno a dos aspectos temáticos:

1.- Actividades en torno a la posibilidad de embaldosar superficies planas con figuras geométricas ( teselaciones ).

2.- Actividades asociadas al diseño, descripción y reconocimiento de transformaciones isométricas

Respecto a la isometría y a las posibilidades de transformaciones de figuras, se pueden describir tres tipos de ejecución: por traslación , por rotación y por simetría (o reflexión ).

Cualquiera que sea el método aplicado para realizar una transformación isométrica en un plano es imprescindible trabajar sobre un sistema de coordenadas .

Sistema de coordenadas

Un sistema de coordenadas bidimensional (en un plano) es un sistema en el cual un punto puede moverse en todas direcciones, manteniéndose siempre en el mismo plano.

El sistema más usado es el sistema de coordenadas rectangular u ortogonal, más conocido como Plano Cartesiano .

Este sistema está formado por dos rectas perpendiculares entre sí llamadas ejes de coordenadas ( eje de las x y eje de las y ).

Las coordenadas de un punto determinan dicho punto. Conocidas las coordenadas de ese punto, puede ser localizado en el plano, como en la figura de abajo donde se han localizado los puntos P1 y P2 . 

 

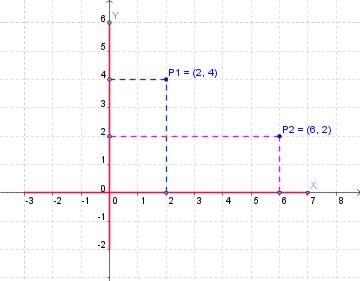
                                                                      Coordenadas para los puntos P1 y P2. 

 

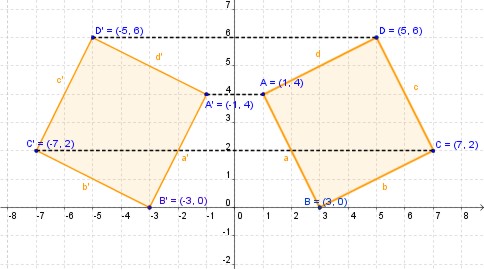
Transformaciones isométricas por Traslación

En una transformación isométrica por traslación se realiza un cambio de posición de la figura en el plano. Es un cambio de lugar, determinado por un vector . 

 

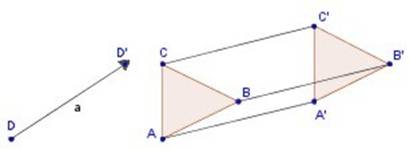
Traslación del punto D a su imagen D’ (vector a = DD’) y Traslación de un triángulo.  

En general, se llama traslación de vector (v) a la isometría que a cada punto m del plano le hace corresponder un punto m' del mismo plano, tal que mm' es igual a v .

Las traslaciones isométricas están marcadas por tres elementos:

La dirección, si es horizontal, vertical un oblicua.

El sentido, derecha, izquierda, arriba y abajo.

Y la magnitud del desplazamiento que se refiere a cuánto se desplazó la figura en una unidad de medida. 

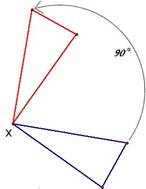
Transformaciones isométricas por Rotación 

 

Rotación del triángulo, respecto del punto X. 

Una rotación , en geometría, es un movimiento de cambio en la orientación de un cuerpo; de forma que, dado un punto cualquiera del mismo, este permanece a una distancia constante de un punto fijo, y tiene las siguientes características:

1. Un punto denominado centro de rotación. 
2. Un ángulo 
3.  Un sentido de rotación.

Estas transformaciones por rotación pueden ser positivas o negativas dependiendo del sentido de giro.

Para el primer caso debe ser un giro en sentido contrario a las manecillas del reloj, y será negativo el giro cuando sea en sentido de las manecillas. 

Transformaciones Isométricas por Simetría

El concepto se simetría se nos presenta de forma natural y nos entrega ejemplos de gran belleza en nuestro entorno.

Simetría en la naturaleza.

 

Tanto la figura del escarabajo como de la mariposa se ven simétricas, pues si trazamos una línea recta en el centro de cada una, la parte que está a la derecha de la línea sería exactamente igual a la parte que está a la izquierda de esa misma línea.

Sobre la base de estos dos ejemplos, se descubre fácilmente que hay una transformación que hace que la parte izquierda de la figura sea un reflejo de la parte derecha sin cambiar su forma ni sus dimensiones. 

Esto nos lleva a afirmar que Simetría es la correspondencia exacta (un reflejo) en la disposición regular de las partes o puntos de un cuerpo o figura con relación a un punto (centro), una recta ( eje de simetría ) o un plano.

Definido o conocido el concepto de simetría , podemos agregar que la simetría puede ser central o axial

Simetría Central

La simetría central , en geometría, es una transformación en la que a cada punto se le asocia otro punto, que debe cumplir las siguientes condiciones:

a) El punto y su imagen estén a igual distancia de un punto llamado centro de simetría .

b) El punto, su imagen y el centro de simetría pertenezcan a una misma recta. 

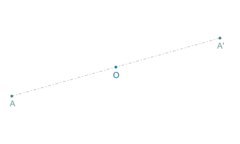
Simetría central del punto A.

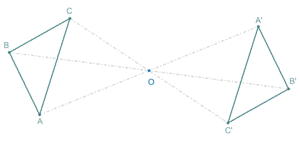
Simetría central del triángulo ABC, respecto del punto O.

 

Según estas definiciones, con una simetría central se obtiene la misma figura con una rotación de 180 grados.

Simetría axial

La simetría axial , en geometría, es una transformación respecto de un eje de simetría , en la cual, a cada punto de una figura se asocia otro punto llamado imagen, que cumple con las siguientes condiciones:

a) La distancia de un punto y su imagen al eje de simetría, es la misma.

b) El segmento que une un punto con su imagen, es perpendicular al eje de simetría. 

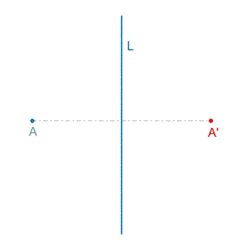
Simetría axial del punto A.

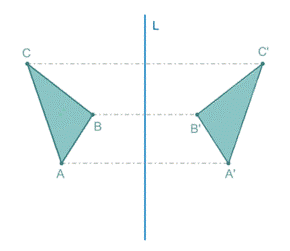
Simetría axial de un triángulo.

 En la simetría axial se conservan las distancias pero no el sentido de los ángulos. El eje de simetría es la mediatriz del segmento AA'. 

 

  La imagen de un objeto reflejada en un espejo plano, es un ejemplo de transformación isométrica: la simetría. 

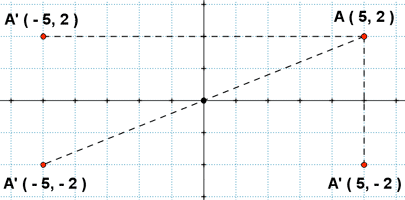
 Simetría de un punto respecto al origen de Coordenadas

Dado un punto P(x,y), su simétrico respecto al origen es el punto P´(-x,-y). Esto es, para determinar las coordenadas del punto simétrico respecto al origen es suficiente con cambiar los signos de las coordenadas del punto P.  

Ejemplo.- Determinar las coordenadas del punto B, simétrico del punto A(4,-3) respecto al origen. 

 Respuesta: Las coordenadas del punto B son: B(-4,3).

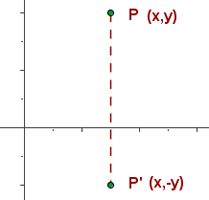
Simetría de un punto respecto al eje de la abscisa

 Dado un punto cualquiera P(x,y ) su simétrico respecto al eje de las abscisas es el P´(x,-y ). Entonces, las abscisas de los puntos P y P´ son iguales, en tanto que para obtener la ordenada del punto P´ es suficiente con cambiar el signo de la ordenada del punto P.  

 

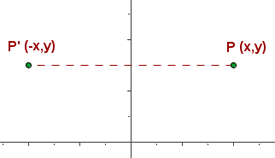
 Simetría de un punto con respecto al eje de la ordenada 

Dado un punto cualquiera P(x,y ) su simétrico respecto al eje de la ordenada es el P´(-x,y ). Entonces, las ordenadas de los puntos P y P´ son iguales, en tanto que para obtener la abscisa del punto P´ es suficiente con cambiar el signo de la abscisa del punto P. 

Traslaciones en el Plano

El hecho de cambiar de posición una figura en un plano llamamos traslación. Se trata de trasladar una figura a un lugar del plano a una distancia, dirección y sentido determinados.

Realizar la traslación de un triángulo a otro lugar del plano tomando como guía un vector.


Solución: 
Vas a ir haciendo paso a paso lo que se te va indicando:

1º : En una hoja de papel cuadrícula dibuja un eje de coordenadas como tienes en F.1.

Señala los puntos:  (-6,-2), (-9,-6) y (-2,-5) que serán los vértices del triángulo

 

 

2º  : Unes los puntos ABC del triángulo y dibujas un vector guía de traslación, lo tienes en color amarillo. Observa que el extremo de este vector tiene de componentes (10,7).
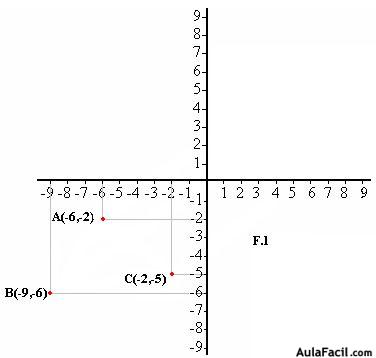
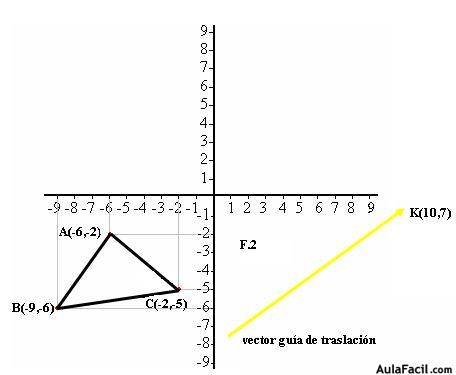
Un modo sencillo de hacer una traslación es servirnos del vector guía. Para ello, a cada punto ABC del triángulo le colocamos el vector guía guardando el mismo módulo, dirección y sentido del vector guía tal como lo tienes en F.3 con los colores verde, rojo y azul.
 

Los extremos de cada uno de los vectores verde, rojo y azul son los nuevos vértices del triángulo.Si sumas las componentes de cada punto A, B y C con los del vector guía tendrás los puntos correspondientes al nuevo triángulo.

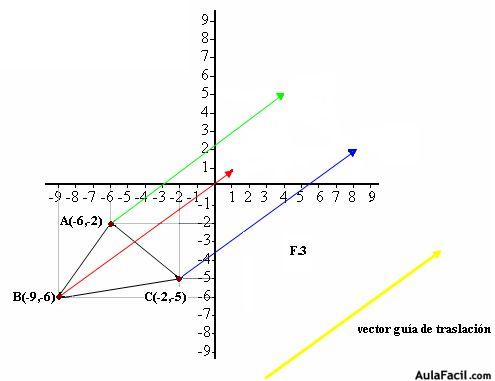
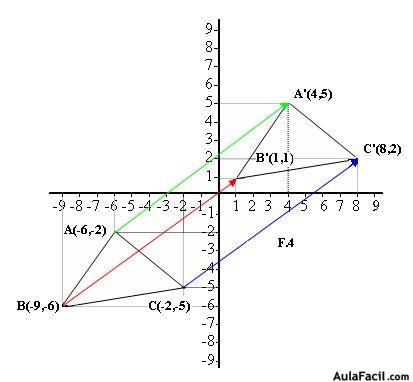
 El triángulo ABC se ha convertido en el A’B’C’ de acuerdo con el vector guía. 
Así pues, los vectores que unen los puntos ABC con A’B’C’ tienen el mismo módulo, dirección y sentido.
Los puntos A’,B’ y C’ son los homólogos de A, B y C, es decir, que están colocados en el mismo orden o posición.

Si sumamos las componentes del punto A = (–6, –2) con  las del  vector guía (10,7)  obtenemos las componentes del punto A’ (–6 + 10, –2 + 7) = A’(4,5) 

Si sumamos las componentes del punto B = (–9, –6) con  las del  vector guía (10,7)  obtenemos las componentes del punto B’ (–9+ 10, –6+ 7) = B’(1,1). 

Si sumamos las componentes del punto C = (–2, –5) con  las del  vector guía (10,7)  obtenemos las componentes del punto C’ (–2+ 10, –5+ 7) = C’(8,2)

 

Rotación o Giro: es un movimiento alrededor de un punto que mantiene la forma y el tamaño de la
figura original.

Una rotación se determina por estos tres elementos:

• Un ángulo que determina la amplitud de la rotación.
• Un punto llamado centro de rotación.
• Un sentido de la rotación que puede ser del mismo sentido de las agujas del reloj o en sentido contrario.

 

 

La vida cotidiana está llena de situaciones en las que la rotación o giro está presente. Cuando abrimos o cerramos una puerta estamos haciendo una rotación sobre un punto o centro de rotación, las ruedas de nuestra bicicleta giran sobre el eje central, al igual que los pedales, giramos al montar en los caballitos, al abrir y cerrar el abanico hacemos que gire sobre un punto, al mover la ruleta hacemos que gire igualmente sobre su centro. 

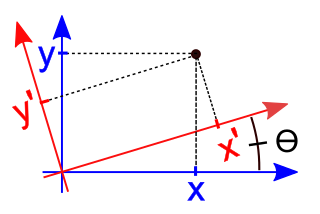
En matemáticas, una rotación de ejes en dos dimensiones es una aplicación de los puntos de un sistema de coordenadas cartesianas xy sobre los puntos de un segundo sistema de coordenadas cartesianas denominado x'y', en la que el origen se mantiene fijo y el los ejes x' e y' se obtienen girando los ejes x e y en sentido contrario a las agujas del reloj a través de un ángulo ${\displaystyle \theta }$. Un punto P tiene coordenadas (x, y) con respecto al sistema original y coordenadas (x', y') con respecto al nuevo sistema.​ En el nuevo sistema de coordenadas, el punto P parecerá haber sido girado en la dirección opuesta, es decir, en el sentido de las agujas del reloj a través del ángulo ${\displaystyle \theta }$. 

Un sistema de coordenadas cartesianas ${\displaystyle xy}$ rotado en un ángulo ${\displaystyle \theta }$, origina un nuevo sistema de coordenadas cartesianas x' y'.

Rotación de Ejes

Cambio de la orientación de los ejes de referencia mientras se conserva el origen. La principal razón para rotar los ejes es que una ecuación dada es mucho más simple en el nuevo sistema de coordenadas que en el sistema original.

Si los ejes originales x y y rotan en sentido contrario al reloj un ángulo , para cualquier punto P(x, y), las coordenadas originales (x, y) se convierten en las nuevas coordenadas (x ´, y ´), que son:

x ´ = x cos + y sen
y´ = - x sen + y cos

 

Ejemplo 1

Encuéntrense las coordenadas del punto ${\displaystyle P_{1}=(x,y)=({\sqrt {3}},1)}$ después de que los ejes hayan sido girados a través del ángulo ${\displaystyle \theta _{1}=\pi /6}$, o 30°.

Solución:

${\displaystyle x'={\sqrt {3}}\cos(\pi /6)+1\sin(\pi /6)=({\sqrt {3}})({\sqrt {3}}/2)+(1)(1/2)=2}$

${\displaystyle y'=1\cos(\pi /6)-{\sqrt {3}}\sin(\pi /6)=(1)({\sqrt {3}}/2)-({\sqrt {3}})(1/2)=0.}$

Los ejes se han girado en sentido contrario a las agujas del reloj en un ángulo de ${\displaystyle \theta _{1}=\pi /6}$ y las nuevas coordenadas son ${\displaystyle P_{1}=(x',y')=(2,0)}$. Téngase en cuenta que el punto parece haberse girado en el sentido de las agujas del reloj a través de ${\displaystyle \pi /6}$ con respecto a los ejes fijos, por lo que ahora coincide con el (nuevo) eje x'. 

Homotecia

Las homotecias transforman una figura plana en otra figura de igual forma, pero de menor o mayor tamaño, según el valor de la razón, k. Si k es positivo la homotecia es directa, y si no, es inversa.

 

Veamos cómo transformar una figura en otra por una homotecia de centro O y razón  k = 1/2.

• Tomamos un punto arbitrario O al que denominaremos centro de homotecia, y trazamos semirrectas con origen en el punto O y que pasen por cada uno de los vértices de la figura dada. 

 

• Sobre una de las semirrectas, por ejemplo la OA, marcamos un punto A′ de modo que se cumpla:

 

• Por el punto A′, trazamos una paralela al lado AB del triángulo hasta cortar la semirrecta OB en el punto B′.

• Por el punto B′, trazamos una paralela al lado BC, hasta cortar la semirrecta OC en el punto C′, y así sucesivamente hasta obtener la nueva figura.

 

Como puedes ver, los vértices homólogos de ambos polígonos están alineados respecto al centro de homotecia O y se cumple:

 

En función del valor de la razón k, tendremos los siguientes casos:

• k > 1 El tamaño de la figura transformada es mayor que el de la original.

 

•  0 < k < 1 El tamaño de la figura transformada es menor que el de la original.

 

•  k < -1 El tamaño de la figura transformada es mayor que el de la original.

 

En una homotecia se cumple:

• El único punto invariante en una homotecia es el centro de homotecia.
• Las rectas que pasan por el centro de homotecia son rectas invariantes.
• Las rectas que contienen segmentos homólogos son paralelas, y la razón de dichos segmentos coincide con la razón de homotecia.

Si aplicamos la definición de homotecia a la figura:

 

Los triángulos OAB y O′A′B′ son semejan­tes, ya que tienen un ángulo en común y tienen los lados proporcionales.
Así pues, se cumplirá que la razón entre los segmentos A′B′ y AB es:

 

 

• Una homotecia conserva el sentido de las figuras.
• Una homotecia de razón k = 1 transforma cada punto en sí mismo. Esta ho­motecia recibe el nombre de identidad (las dos figuras coinciden).
  
• Si la razón de una homotecia es k = -1, se trata de una simetría central.

 

 

Haga Click Aqui para ver un video sobre homtecia

 Haga Click Aquí para la práctica 1

Ejercicios:

1- Dibuja una reflexión de la figura sobre el eje x , sobre el eje y  y sobre el origen del coordenadas O

x−x

2-  Instrucciones : Usa esta figura para responder cada pregunta. Siempre que sea posible, escribe todo en notación cartesiana. 

 

1. Traslada esta figura tres unidades hacia arriba.

2. Traslada esta figura cuatro unidades a la derecha.

3. Traslada esta figura cinco unidades hacia abajo.

4. Traslada esta figura seis unidades a la izquierda.

5. Traslada esta figura una unidad hacia abajo y dos unidades a la derecha.

6. Traslada esta figura dos unidades hacia arriba y una unidad a la izquierda.

7. Traslada esta figura tres unidades hacia arriba y una unidad a la derecha.

8. Rota esta figura en 180 grados.

9. Rota esta figura en 90 grados.

10. Refleja esta figura sobre el eje x .

11. Refleja esta figura sobre el eje y .

12. Traslada esta figura cinco unidades hacia arriba y tres unidades a la derecha.

13. Traslada esta figura seis unidades hacia abajo y cuatro unidades a la izquierda.

14. Verdadero o Falso. La figura de abajo es un reflejo de la original.

   

15. Verdadero o Falso. Esta figura fue rotada en 180∘ . 

 

Click Aquí para la práctica de homotecia

 

 

 

 

 

 

 

 

 

${\displaystyle x'y'}$