Unidad V: Los Polígonos

 

 Polígonos – Definición de polígono

Un polígono es el área de un plano que está delimitado por líneas que tienen que ser rectas.

Si hacemos caso a la etimología de la palabra, polígono proviene de los términos griegos «poli» y «gono«. «Poli» podría traducirse como «muchos» y «gono» como «ángulo». Atendiendo a esto podríamos decir que un polígono es literalmente aquello que tiene muchos ángulos.

Para considerar polígono a una figura esta debe cumplir que sus líneas siempre deben ser rectas y que no puede estar abierto. En la siguiente imagen puedes ver varios ejemplos de polígonos y otros que no lo son:

 

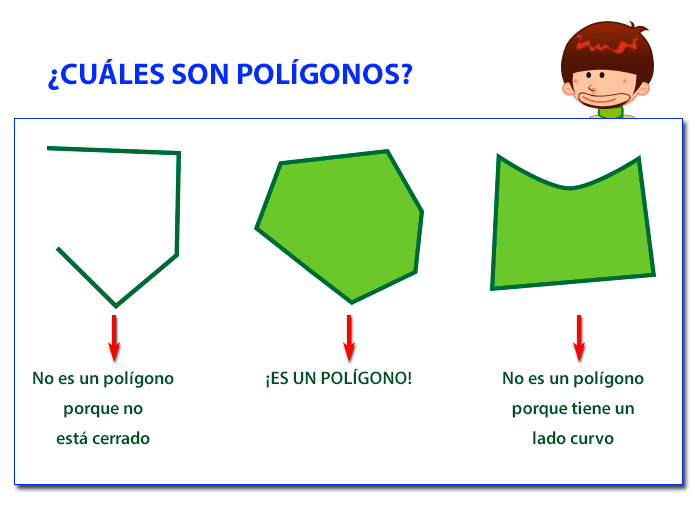
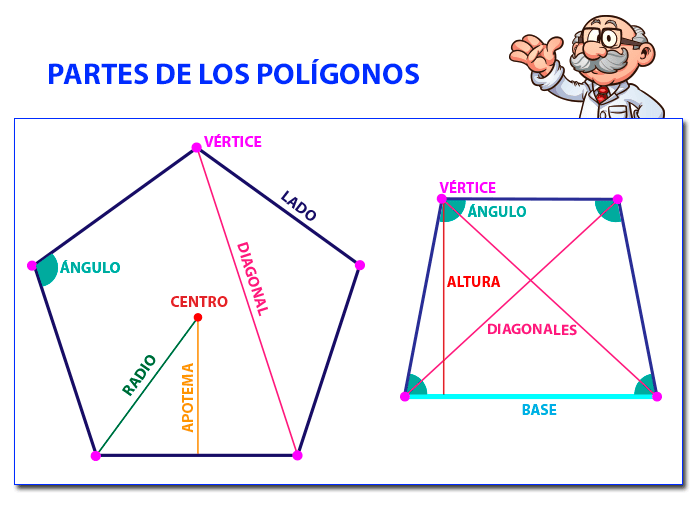
• Lados: son los segmentos que forman la línea poligonal.
• Vértices: son los puntos donde se unen los lados.
• Ángulos: son las regiones del plano que delimitan dos lados.
• Diagonal: es la recta que une dos vértices no consecutivos.
• Centro: es el punto desde el que todos los ángulos y lados están a la misma distancia.
• Radio: es el segmento que une el centro del polígono con cualquiera de sus vértices
• Apotema: es el segmento que une el centro del polígono con el centro de cualquiera de sus lados.
• Base: Es el lado inferior de un polígono. Normalmente es el lado donde se «apoya» la figura.

CClasificación de polígonos

Podemos clasificar los polígonos de tres formas diferentes:

• Clasificación de polígonos según sus lados:

  • Triángulo:  3 lados
  • Cuadrilátero: 4 lados
  • Pentágono: 5 lados
  • Hexágono: 6 lados
  • Heptágono: 7 lados
  • Octógono: 8 lados
  • Eneágono: 9 lados
  • Decágono: 10 lados
  • Endecágono: 11 lados
  • Dodecágono: 12 lados

• Clasificación de polígonos según sus ángulos:

  • Polígonos cóncavos: es cuando el polígono tiene un ángulo que mide más de 180º.
  • Polígonos convexos: es cuando todos los ángulos del polígono miden menos de 180º.

• Clasificación de polígonos según sus lados y sus ángulos:

  • Polígonos regulares: es cuando un polígono tiene todos sus lados y ángulos iguales.
  • Polígonos irregulares: es cuando en un polígono hay uno o más lados y/o ángulos que no son iguales.
  Click Aquí para ver el siguiente video sobre la clasificación de los polígonos 

CLASIFICACIÓN DE POLÍGONOS SEGÚN SUS LADOS
TRIÁNGULO	CUADRILÁTERO
PENTÁGONO	HEXÁGONO
HEPTÁGONO	OCTÓGONO
ENEÁGONO	DECÁGONO
ENDECÁGONO	DODECÁGONO
CLASIFICACIÓN DE POLÍGONOS SEGÚN SUS ÁNGULOS
POLÍGONOS CÓNCAVOS	POLÍGONOS CONVEXOS
CLASIFICACIÓN DE POLÍGONOS SEGÚN SUS LADOS Y SUS ÁNGULOS
POLÍGONOS REGULARES	POLÍGONOS IRREGULARES

 

Perímetro y área de los polígonos

Perímetro de un polígono

Calcular el perímetro de los polígonos es muy sencillo, tan solo debemos sumar la medida de cada uno de sus lados. Cuando se trata de polígonos regulares, en los que todos sus lados miden lo mismo, tan solo tendremos que multiplicar el largo de uno de ellos por el número total de lados del polígono.

Si el polígono es irregular tendremos que sumar la medida de cada uno de sus lados para hallar el perímetro total.

En la siguiente imagen verás algunos ejemplos:

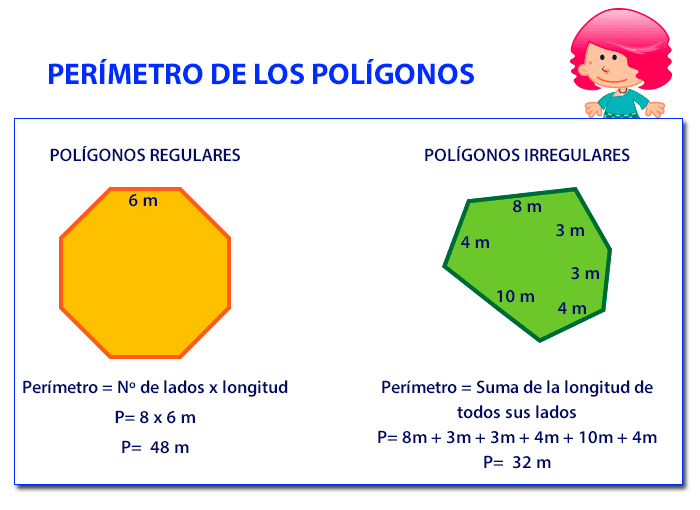
 Como vemos en la imagen el primer polígono (el de color anaranjado) es un polígono regular, concretamente un octógono. Para este tipo de polígonos tan solo es necesario conocer la medida de uno de sus lados, ya que todos los demás medirán lo mismo. Después tan solo debemos multiplicar esta medida por el número total de lados.

En el caso del polígono verde, se trata de un polígono irregular por lo que para calcular su perímetro debemos sumar la longitud de cada uno de sus lados.

Área de un Polígono

Cuando pintamos una pared, alicatamos un suelo o compramos un mantel para la mesa, debemos conocer su medida para comprar la cantidad adecuada de pintura, azulejos o tela.

A esa medida la llamamos área. Y ahora, vamos a aprender a calcular el área de diferentes polígonos. Pero antes comencemos conociendo qué es la superficie.

La superficie es una región de plano comprendida entre una línea poligonal cerrada o una circunferencia. Por lo tanto, a la medida de esta superficie la llamamos área, y la expresamos en unidades de superficie. La unidad básica de superficie es el metro cuadrado (m²)

Dado que existen diferentes polígonos, la forma de hallar su área, también será diferente. Lo mejor es empezar conociendo cómo se obtiene el área de un rectángulo.

Para calcular el área de un rectángulo debemos conocer la longitud de su base, largo, y de su altura o ancho; y después multiplicarlas.  Así de fácil.

ÁREA = BASE X ALTURA

ÁREA = b x h

ÁREA = 9 cm x 3 cm

ÁREA = 27 cm²

El área de un cuadrado tiene relación con el del rectángulo. Al igual que este sería base por altura, pero ya que todos los lados de un cuadrado miden lo mismo, podemos decir que el área de un cuadrado es su lado elevado al cuadrado, o lo que es lo mismo lado por lado.

 

 

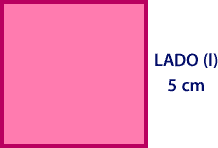
ÁREA = b x h => ÁREA = LADO X LADO

ÁREA = l²

ÁREA = 5 cm x 5 cm = 25 cm²

ÁREA = 5² = 25 cm²

El área de romboides, triángulos y rombos está estrechamente relacionada con el área del rectángulo. Recuerda que el área de un rectángulo es base por altura.

Empecemos por el área del romboide. Si te fijas bien, con un poco de paciencia y buena mano podemos convertir cualquier romboide en un rectángulo.

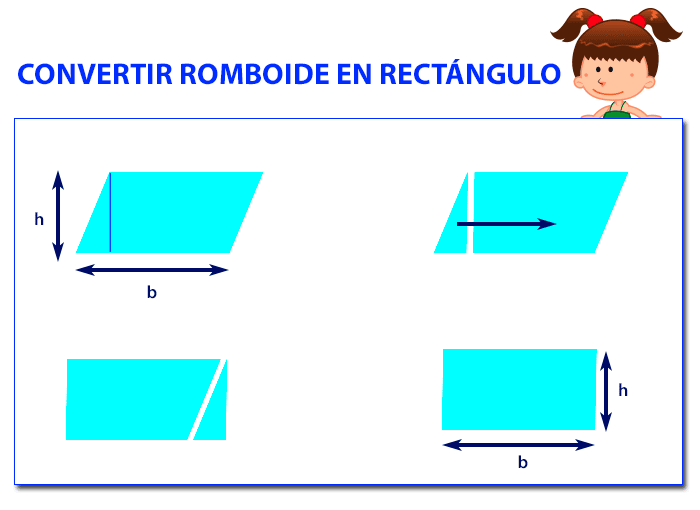
Por lo tanto, el área de un romboide será base por altura

 

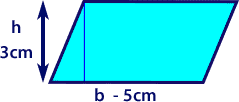
ÁREA = base x altura

ÁREA = b x h

ÁREA = 5cm x 3cm = 15cm²

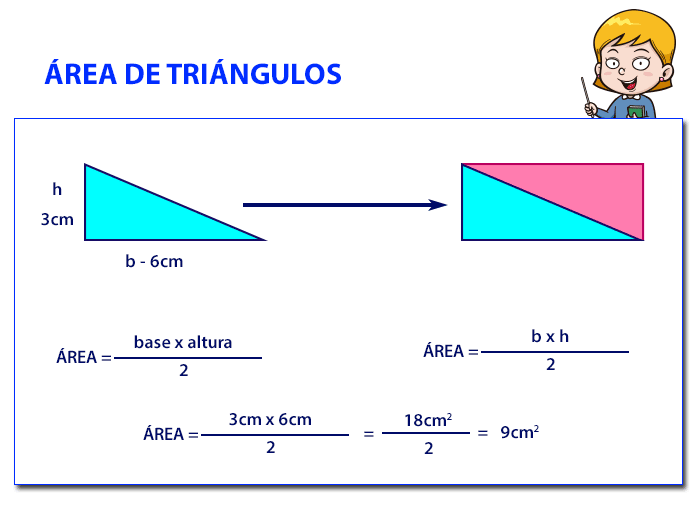
Continuemos con el área del triángulo. Mira qué pasa si englobamos estos triángulos en rectángulos o romboides. El triángulo es la mitad del rectángulo o del romboide. De esa forma el área del triángulo, será base por altura dividido entre dos, al ser la mitad que un rectángulo o romboide .

 

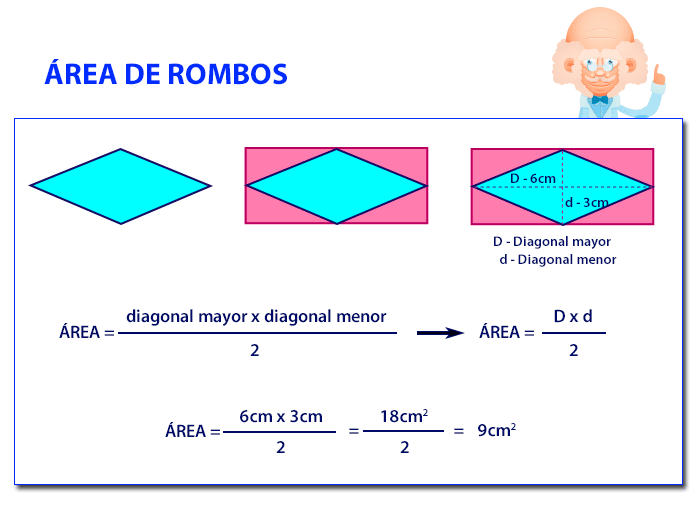
Vamos a calcular ahora el área de un rombo. Estas figuras planas también pueden englobarse en un rectángulo, y si dibujamos las diagonales  y tenemos en cuenta los triángulos obtenidos, nos damos cuenta que el romboide es exactamente la mitad de un rectángulo. Por lo tanto su área será la mitad que la de un rectángulo, es decir diagonal mayor por diagonal menor dividido entre dos.

  Ahora te enseñaremos cómo calcular el área de los polígonos regulares. Todas los polígonos pueden descomponerse en triángulos uniendo el centro con sus vértices. Por lo que para calcular el área, sólo tendríamos que hallar el área de uno de los triángulos en que hemos descompuesto la figura, y multiplicarlo por el número de triángulos obtenidos. Pero esta operación se puede simplificar, siendo el área de un polígono regular el perímetro por la apotema dividido entre 2.   Recuerda que el perímetro es la suma de todos sus lados y el apotema es la distancia del centro al punto medio de un lado.

 

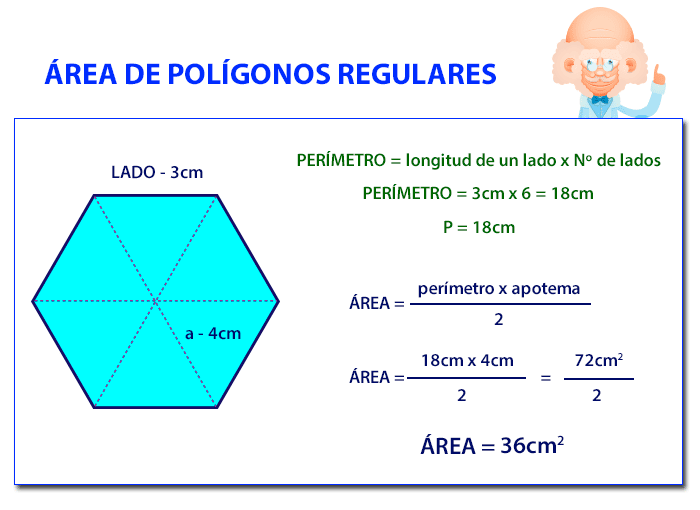
Propiedades de los polígonos

Vamos a ver ahora algunas de las propiedades de los polígonos:

• En un polígono coincide que sus lados, vértices, ángulos interiores, ángulos exteriores y ángulos centrales son iguales. A este dato se le conoce como «n». Es decir un héxagono, por ejemplo, tendrá 6 lados, 6 vértices, 6 ángulos interiores, 6 ángulos exteriores y 6 ángulos centrales. Para el caso del hexágono n=6
• La suma de los ángulos interiores de un polígono de n lados es 180°(n-2)

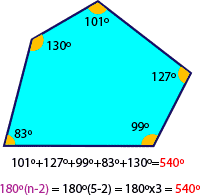
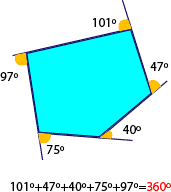
• En un polígono convexo, la suma de los ángulos exteriores es simpre 360°

• El número de diagonales de un polígono es Nd=n(n-3)/2

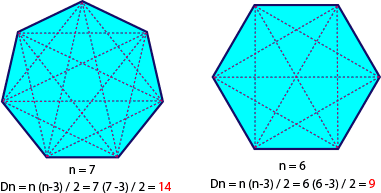
• A partir de un vértice de un polígono, se pueden trazar (n-3) diagonales.

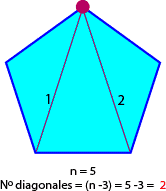
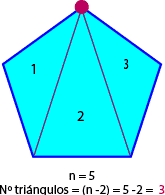
• Al trazar diagonales desde un mismo vértice se obtiene (n-2) triángulos.

 

Práctica 1 Sobre Polígonos: