Unidad VII: Los Poliedros

Poliedro

Un poliedro, en el área de la geometría euclidiana, es definido como un objeto tridimensional que está compuesto por un número finito de superficies poligonales o, en otras palabras, de caras. Técnicamente, un poliedro es el límite entre el interior y el exterior de un sólido. En general, los poliedros se nombran según el número de caras que tengan. Un tetraedro tiene cuatro caras, un pentaedro cinco, y así sucesivamente; un cubo es un poliedro regular de seis lados (hexaedro) cuyas caras son cuadradas. Las caras se encuentran en segmentos de línea llamados bordes, que se encuentran en los puntos llamados vértices.

Sección 1: Definición e historia - Poliedros - Unidad didáctica

Elementos de un Poliedro

En un poliedro podemos distinguir los siguientes elementos:

Caras: son los polígonos que forman el poliedro.
Aristas: son los segmentos en los que se intersecan (cortan) las caras.
Vértices: son los puntos donde se intersecan las aristas.

Además podemos citar los ángulos diedros delimitados por dos caras que se cortan y los ángulos poliedros determinados por las caras que inciden en un mismo vértice

Poliedros: figuras básicas y clasificación

Tipos de Poliedros

Los tipos de poliedro que existen son los siguientes:

Poliedro regular

Un poliedro regular es el cual en sus caras son todas polígonos regulares y además son todas iguales. Las aristas también son todas iguales y existen únicamente cinco tipos de poliedros regulares:

Tetraedro regular: es un poliedro regular cuya superficie se encuentra formada por cuatro triángulos equiláteros del mismo tamaño.
Cubo (o hexaedro regular): está compuesto por seis cuadrados iguales.
Octaedro regular: la superficie está constituida por ocho triángulos equiláteros iguales
Dodecaedro regular: esta formado por doce pentágonos regulares iguales
Icosaedro regular: es un poliedro regular en el cual las caras son veinte triángulos equiláteros todos ellos iguales.

Poliedro Irregular

Los irregulares son aquellos cuyas caras son polígonos pero que no son todos iguales. Entre ellos podemos mencionar los sólidos arquimedianos que son poliedros convexos de caras regulares, pero no uniformes. Se clasifican principalmente por el número de caras que tiene su superficie:

Tetraedro: poliedro irregular con cuatro caras
Pentaedro: irregular con cinco caras
Hexaedro: irregular con seis caras
Heptaedro: irregular con siete caras
Octaedro: poliedro irregular con ocho caras
Eneaedro: irregular con nueve caras
Decaedro: irregular con diez caras

Además, existen dos casos muy especiales de tetraedro irregular son:

Tetraedro trirrectángulo: es el que tiene tres caras que son triángulos rectángulos, en los que sus ángulos rectos concurren a un mismo vértice.
Tetraedro isofacial: es un tetraedro irregular cuya base es un triángulo rectángulo y sus tres caras laterales son tres triángulos isósceles iguales.
Convexos: se forman cuando cualquier par de puntos del espacio que estén dentro del cuerpo los une un segmento de recta también interno.
Poliedro de caras regulares: cuando todas las caras del mismo son polígonos regulares.
Poliedro de caras uniformes: cuando todas las caras son iguales.

Características

Las principales características del poliedro son las siguientes:

Sus caras son planas.
Tiene un volumen finito de superficies planas.
Son cuerpos tridimensionales.
Se nombran dependiendo del número de caras que posean: tetraedro, pentaedro, hexaedro, heptaedro, icosaedro.

Area y Volumen de Poliedros

Recordemos antes los elementos del prisma:

Las fórmulas generales para obtener el área y el volumen de cualquier prisma son las siguientes:

Resolvamos ejercicios de ejemplos específicos.

1.- Hallar el área total y el volumen de un prisma triángular cuya base mide 10 x 43 y con una altura de 42 cm; si la altura el prisma mide 60 cm.

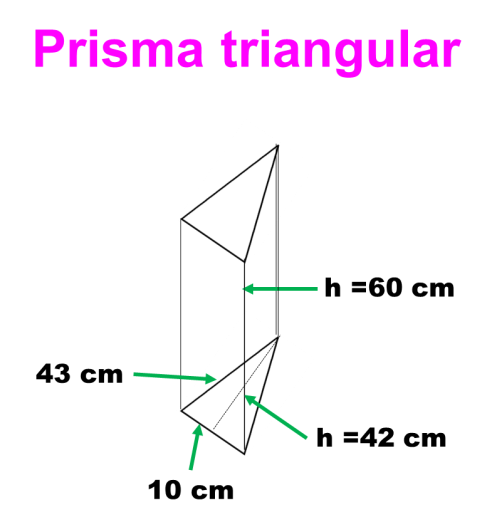
Obtengamos primero el área lateral (el de las tres caras) que es el área coloreada.

prismas_4

Y ahora el área de las bases. Para ello en la fórmula general vamos a sustituir por la fórmula para obtener el área de un triángulo, ya que la base es triangular; y después el resultado se multiplicará por 2 (ya que el prisma tiene dos bases iguales, en este caso, triángulos isósceles). Es el área coloreada.

prismas_5

Por último sumaremos los valores del área lateral y del área de las dos bases para obtener el área total del prisma triangular especificado.

PRISMA_6

Ahora obtenemos el volumen del prisma triangular sustituyendo la fórmula del área de la base por la del área del triángulo y multiplicando por la altura del poliedro.

2.- Hallar el área total y el volumen de un prisma cuadrangular regular cuyo lado de la base mide 1.20 m y la altura de 4 m.

Nos enfocamos en la forma de las bases del prisma para despejar estas fórmulas. El problema indica que es un prisma cuadrangular regular; que es el prisma que tiene como bases dos cuadrados y sus caras son cuatro rectángulos iguales.

área_volumen_prismas8

Obtengamos primero el área lateral (el de las cuatro caras rectangulares iguales) que es el área coloreada.

área_volumen_prismas9

Y ahora el área de las bases. Para ello en la fórmula general vamos a sustituir por la fórmula para obtener el área de un cuadrado, ya que la base es cuadrangular; y después el resultado se multiplicará por 2 (ya que el prisma tiene dos bases iguales, en este caso, cuadrados). Es el área coloreada.

área_volumen_prismas10

Por último sumaremos los valores del área lateral y del área de las dos bases para obtener el área total del prisma cuadrangular regular especificado.

Ahora obtenemos el volumen del prisma cuadrangular regular sustituyendo la fórmula del área de la base por la del área del cuadrado y multiplicando por la altura del poliedro.

área_volumen_prismas12

3.- Hallar el área total y el volumen de un prisma cuadrangular irregular cuya base mide 38 cm por 21 cm y la altura del prisma es de 30 cm.

Nos enfocamos en la forma de las bases del prisma para despejar estas fórmulas. El problema indica que es un prisma cuadrangular irregular; que es el prisma que tiene como bases dos cuadriláteros que pueden ser rectángulos, rombos, romboides, trapecios o trapezoides; y sus caras son cuatro rectángulos. En este caso las bases son rectángulos.

área_volumen_prismas13

Obtengamos primero el área lateral (el de las cuatro caras rectangulares) que es el área coloreada.

área_volumen_prismas14

Y ahora el área de las bases. Para ello en la fórmula general vamos a sustituir por la fórmula para obtener el área de un rectángulo, ya que la base es rectangular; y después el resultado se multiplicará por 2 (ya que el prisma tiene dos bases iguales, en este caso, rectángulos). Es el área coloreada.

área_volumen_prismas15

Por último sumaremos los valores del área lateral y del área de las dos bases para obtener el área total del prisma rectangular especificado.

área_volumen_prismas16

Ahora obtenemos el volumen del prisma rectangular sustituyendo la fórmula del área de la base por la del área del rectángulo y multiplicando por la altura del poliedro.

área_volumen_prismas17

4.- Hallar el área total y el volumen de un prisma pentagonal regular cuya base mide 7.265 de lado y 5cm de apotema, y la altura el prisma mide 14 cm.

Nos enfocamos en la forma de las bases del prisma para despejar estas fórmulas. El problema indica que es un prisma pentagonal regular con las siguientes medidas.

Obtengamos primero el área lateral (el de las cinco caras rectangulares) que es el área coloreada.

Y ahora el área de las bases. Para ello en la fórmula general vamos a sustituir por la fórmula para obtener el área de un pentágono, ya que la base es pentagonal; y después el resultado se multiplicará por 2 (ya que el prisma tiene dos bases iguales, en este caso, pentágonos regulares). Es el área coloreada.

Por último sumaremos los valores del área lateral y del área de las dos bases para obtener el área total del prisma pentagonal regular especificado.

Ahora obtenemos el volumen del prisma pentagonal regular sustituyendo la fórmula del área de la base por la del área del pentágono y multiplicando por la altura del poliedro.

Cuerpos Redondos

Son la Esfera, el Cono y el Cilindro. Los cuerpos redondos son aquellos que tienen, al menos, una de sus caras o superficies de forma curva. También se denominan cuerpos de revolución porque pueden obtenerse a partir de una figura que gira alrededor de un eje.

Cuerpos redondos

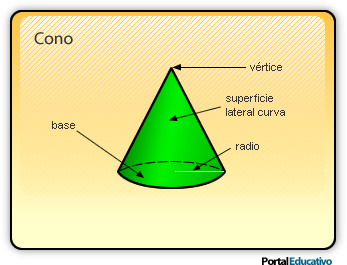
Cono

El cono es un cuerpo geométrico generado por un triángulo rectángulo al girar en torno a uno de sus catetos.

Cono

Elementos del cono
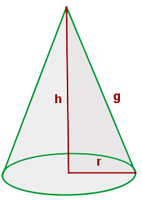
En la imagen superior, podemos distinguir los elementos de un cono recto:

- Eje: es el cateto AC. Alrededor de él gira el triángulo rectángulo.
- Base: es el círculo que genera la rotación del otro cateto, AB. Por lo tanto AB es el radio del cono. La base se simboliza: O (A, AB).
- Generatriz: es la hipotenusa del triángulo rectángulo, BC, que genera la región lateral conocida como manto del cono.
- Altura: corresponde al eje del cono, porque une el centro del círculo con la cúspide siendo perpendicular a la base.

El cono tiene una cara basal plana y una cara lateral curva. Posee una arista basal y un vértice llamado cúspide.

Elementos del cono

El Cilindro

El cilindro es el cuerpo geométrico generado por un rectángulo al girar en torno a uno de sus lados.

Cuerpos redondos

Elementos del cilindro

Por medio del dibujo de arriba, es posible determinar los elementos de un cilindro, que son: eje, bases, altura y generatriz.

- Eje: lado AD, alrededor del cual gira el rectángulo.

- Bases: son los círculos paralelos y congruentes que se generan al girar los lados AB y CD del rectángulo. Cada uno de estos lados es el radio de su círculo y también, el radio del cilindro.

- Altura: corresponde al mismo eje AD; es perpendicular a las bases y llega al centro de ellas. Esta es la razón por la que el cilindro es recto.

- Generatriz: es el lado BC, congruente con el lado AD, y que al girar forma la cara lateral o manto del cilindro.

El cilindro tiene 2 caras basales planas, paralelas y congruentes. 1 cara lateral que es curva y 2 aristas basales.

Puedes observar que en el desarrollo en el plano se forma un rectángulo para la cara lateral, cuyos lados son el perímetro de la circunferencia que forma las bases y la altura o generatriz.

cilindro

Cuerpos redondos

La Esfera

Una superficie esférica es la superficie engendrada por una circunferencia que gira sobre su diámetro. Una esfera es la región del espacio que se encuentra en el interior de una superficie esférica.

Los elementos notables de una esfera son:

imagen

El centro es el punto interior que equidista de cualquier punto de la esfera.
El radio es la distancia del centro a un punto de la esfera.
La cuerda es el segmento que une dos puntos cualesquiera de la superficie.
El diámetro es la cuerda que pasa por el centro.
Los polos son los puntos del eje de giro que quedan sobre la superficie esférica.

Además de estos elementos notables, en la esfera también podemos encontrar circunferencias notables que son necesarias conocer:

imagen

Los paralelos son las circunferencias obtenidas al cortar la superficie esférica con planos perpendiculares al eje de revolución.
El ecuador es la circunferencia obtenida al cortar la superficie esférica con el plano perpendicular al eje de revolución que contiene al centro de la esfera.
Los meridianos son las circunferencias obtenidas al cortar la superficie esférica con planos que contienen el eje de revolución.

Figuras geométricas en la Esfera

Hemisferio: Es cada una de las partes en que queda dividida la superficie esférica por un plano que pasa por el centro de la esfera, llamado plano diametral.

Semiesfera: Parte de una esfera comprendida entre dos planos que se cortan en el diámetro de aquella.

Huso esférico: El huso esférico es la parte de la superficie de una esfera comprendida entre dos planos que se cortan en el diámetro de aquella.

Cuña esférica: La cuña esférica es la parte de una esfera comprendida entre dos planos que se cortan en el diámetro de aquella.

Casquete esférico: Un casquete esférico es cada una de las partes de la esfera determinada por un plano secante.

Zona esférica: Una zona esférica es la parte de la esfera comprendida entre dos planos secantes paralelos.

imagen

Area y Volumen de Cuerpos Redondos

Area del Cilindro: el area del cilindro comprende el área lateral y el área de las dos bases.

Área lateral = perímetro de la base x altura

A _lateral = 2 π r . h

Si a la expresión anterior le sumamos el área de las dos regiones circulares basales, obtenemos el área total del cilindro:

Área total = área lateral + 2 x área de la base

Entonces,

A _total = 2 Π r h + 2 Π r ²

Por lo tanto:

A _total = 2 Π r ( h + r )

Volumen del cilindro

Para un cilindro circular, su volumen (V) es igual al producto del área del círculo basal por su altura (h).

Para calcular su volumen se emplea la siguiente fórmula:

Volumen del cilindro = área de la base x altura

V _cilindro = Π r ² · h

Ejemplo:

¿Cuál es el área total de un cilindro si su radio basal mide 10 cm y su altura mide 20 cm?

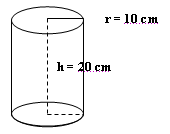
cilindro002

Se sabe que: r = 10 cm y h = 20 cm

2 Π · 10 cm (20 cm + 10 cm) = 20 Π cm (30 cm) = 600 Π cm ²

A _total = 600 Π cm ² = 600 x 3,14 = 1.884 cm ²

¿Cuál es el volumen del cilindro anterior?

Se sabe que: r = 10 cm y h = 20 cm

Π (10 cm) ² · 20 cm = 2000 Π cm ³ = 6.283 cm ³

V _cilindro = 6.283 cm ³

^{Area y Volumen de un Cono}

En las siguientes fórmulas ${g, A_{L}, A_{T}, V}$ representan la generatriz, área lateral, área total y volumen de la figura, respectivamente.

Formula de areay volumen del cono

${g^{2}=h^{2}+r^{2}}$

${A_{L}=\pi r g}$

${A_{T}=\pi r (g+r)}$

${V=\displaystyle\frac{\pi r^{2} h}{3}}$

^{Para el caso de un Tronco de Cono se tiene:}

Formula de areay volumen del tronco del cono

${A_{L}=\pi g(R+r) }$

${A_{T}=\pi [g(R+r)+R^{2}+r^{2}]}$

${V=\displaystyle\frac{1}{3}\pi h (R^{2}+ r^{2}+Rr)}$

Ejercicios Resueltos

1) Calcula el área lateral, total y el volumen de un cono cuya generatriz mide 13 cm y el radio de la base es de 5 cm.

2) Calcula el área lateral, total y el volumen de un cono cuya altura mide 4 cm y el radio de la base es de 3 cm.

3) Calcular el área lateral, el área total y el volumen de un tronco de cono de radios 6 y 2 cm, y de altura 10 cm.

4) Calcular el área lateral, el área total y el volumen del tronco de cono de radios 12 y 10 cm, y de generatriz 15 cm.

Area y Volumen de una Esfera y una Semiesfera

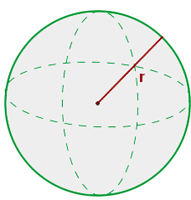
La esfera es el espacio geométrico de puntos que equidistan a un mismo punto que se denomina centro. El radio es la distacia entre el centro y un punto de la esfera, y se denota $r$ .

esfera representación gráfica

Área de una esfera

$\displaystyle A=4\cdot \pi \cdot r^2$

Volumen de una esfera

$\displaystyle V=\frac{4}{3}\cdot \pi \cdot r^3$

Semiesfera

Es cada una de las partes en que queda dividida la superficie esférica por un plano que pasa por el centro de la esfera, llamado plano diametral. También se le conoce como hemisferio.

hemisferio representación gráfica

Área de la semiesfera

$\displaystyle A=2\cdot \pi \cdot r^2$

Volumen de la semiesfera

$\displaystyle V=\frac{2}{3}\pi\cdot r^3$

Ejemplos

1) Calcular el área y el volumen de una esfera inscrita en un cilindro de 2 m de altura.

2) Calcular el volumen de una semiesfera de 10 cm de radio.

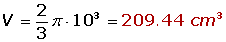
3) Calcular el área del círculo resultante de cortar una esfera de 35 cm de radio mediante un plano cuya distancia al centro de la esfera es de 21 cm.

Huso esférico

huso esferico representación gráfica

El huso esférico es la parte de la superficie de una esfera comprendida entre dos planos que se cortan en el diámetro de aquella.

cuña esférica representación gráfica

Área del huso esférico

$\displaystyle A=\frac{4\cdot \pi \cdot r^2}{360}\cdot n$

Volumen de la cuña esférica

$\displaystyle V=\frac{4}{3}\cdot \frac{\pi\cdot r^3}{360}\cdot n$

Casquete esférico

Un casquete esférico es cada una de las partes de la esfera determinada por un plano secante.

$\displaystyle R=\frac{r^2+h^2}{2h}$

Área del casquete

$A=2\cdot \pi \cdot R \cdot h$

Volumen del casquete esférico

$V=\frac{1}{3}\pi\cdot h^2 \cdot (3R-h)$

Zona Esférica

Una zona esférica es la parte de la esfera comprendida entre dos planos secantes paralelos.

Área de la zona esférica

$\displaystyle A=2\cdot \pi \cdot R \cdot h$

Volumen de la zona esférica

$\displaystyle V=\frac{1}{6}\pi \cdot h \cdot (h^2+3\cdot R^2+3r^2)$

Ejemplos Resueltos

1) Calcula el área y el volumen del siguiente casquete esférico.

2) Calcular el área y el volumen de una zona esférica cuyas circunferencias tienen de radio 10 y 8 cm, y la distancia entre ellas es de 6cm.

3) Un cubo de 20 cm de arista está lleno de agua. ¿Cabría esta agua en una esfera de 20 cm de radio?

4) La cúpula de una catedral tiene forma semiesférica, de diámetro 50 m. Si restaurarla tiene un coste de 300 € el m², ¿A cuánto ascenderá el presupuesto de la restauración?

Matemática CVA

Buscar este blog