Unidad III: Triángulos, Líneas Notables Y Congruencias

 

TRIÁNGULOS

 

        Un triángulo es el polígono que resulta de unir 3 puntos con líneas rectas.

        Todo triángulo tiene 3 lados (a, b y c), 3 vértices (A, B y C) y 3 ángulos interiores (A, B y C)

        Habitualmente se llama lado a al lado que no forma parte del ángulo A. Lo mismo sucede con los lados b y c y los ángulos B y C.

 

 

Los triángulos podemos clasificarlos según 2 criterios:

 

Según la medida de sus lados

 

- Equilátero

            Los 3 lados (a, b y c) son iguales             

            Los 3 ángulos interiores son iguales

 

 

- Isósceles

            Tienen 2 lados iguales (a y b) y un lado distinto (c)

            Los ángulos A y B son iguales, y el otro agudo es distinto

 

 

- Escaleno

            Los 3 lados son distintos

            Los 3 ángulos son también distintos

 

 

Según la medida de sus ángulos

 

- Acutángulo

            Tienen los 3 ángulos agudos (menos de 90 grados)

 

 

- Rectángulo

            El ángulo interior A es recto (90 grados) y los otros 2 ángulos son agudos

            Los lados que forman el ángulo recto se llaman catetos (c y b), el otro lado hipotenusa

 

 

- Obtusángulo

            El ángulo interior A es obtuso (más de 90 grados)

            Los otros 2 ángulos son agudos

 

 

Lineas y Puntos Notables del Triángulo 

Entre las rectas notables más conocidas de un triángulo veremos las mediatrices, las medianas, las alturas y las bisectrices; Y, sobre sus puntos notables asociados: el circuncentro, el baricentro, el ortocentro y el incentro y exincentros, respectivamente.

Mediatrices y circuncentro

 Las mediatrices de un triángulo son las mediatrices de sus lados, es decir, las rectas que pasan por el punto medio de cada uno de sus lados y son perpendiculares a los mismos.

 

 

La mediatriz de un segmento cualquiera es el lugar geométrico de los puntos del plano que equidistan (están a la misma distancia) de los puntos extremos de dicho segmento. En el caso del lado de un triángulo es, por tanto, el lugar geométrico de los puntos que equidistan de los vértices de dicho lado.

Las tres mediatrices del triángulo (hay una por cada lado) se cortan en un punto que está, por tanto, a la misma distancia de los tres vértices del triángulo. Eso quiere decir que se puede trazar una circunferencia con centro en dicho punto y que pase por los tres vértices. A esa circunferencia se la denomina circunferencia circunscrita, y al centro de la misma en el que se cortan las tres mediatrices circuncentro.

 

Bisectrices, Incentro y Exincentros

Las bisectrices de un triángulo son las bisectrices de sus ángulos. Existen bisectrices internas (las usuales) y externas a estos ángulos, y son perpendiculares entre sí.

 

 

La bisectriz de un ángulo es el lugar geométrico de los puntos del plano que equidistan de los dos lados del ángulo.

Las tres bisectrices interiores del triángulo (hay una por cada ángulo) se cortan en un punto que está, por tanto, a la misma distancia de los tres lados del triángulo. Eso quiere decir que se puede trazar una circunferencia con centro en dicho punto y que sea tangente a los tres lados del triángulo. A esa circunferencia se la denomina circunferencia inscrita, y al centro de la misma en el que se cortan las tres bisectrices incentro.

Además, las bisectrices exteriores de dos ángulos concurren con la bisectriz interior del ángulo restante en puntos denominados exincentros, que son los centros de las circunferencias exinscritas del triángulo. Hay 3 exincentros, al igual que 3 circunferencias exinscritas. Las circunferencias exinscritas son tangentes a un lado y a la extensión de los otros dos.

 

 

 

Medianas y Baricentro

 Las medianas de un triángulo son las rectas que pasan por uno de sus vértices y por el punto medio del lado opuesto a dicho vértice.

Las tres medianas de un triángulo se cortan en un punto llamado baricentro o centroide, G.

 

Se cumple que el baricentro divide a cada mediana con razón 2:1, de manera que la distancia desde el baricentro a cada vértice es el doble que la distancia al punto medio del lado opuesto.

 

Además, cada mediana del triángulo lo divide en dos triángulos de igual área, y las tres medianas dividen al triángulo en 6 triángulos de áreas iguales.

También puedes observar otra cosa: uniendo los pies de las medianas (punto medio de cada lado) se obtiene un triángulo semejante al original con área 1/4 del área de éste.

 

 En algunos países a las medianas se las llama transversales de gravedad, y esto se debe a que el baricentro coincide con el centro de gravedad del triángulo. Es decir, si cortas un triángulo, por ejemplo, en una cartulina y lo sujetas colgando de un hilo justo en su baricentro, el triángulo se mantiene en equilibrio.

Alturas y Ortocentro

 Las alturas de un triángulo son las rectas que pasan por uno de sus vértices y son perpendiculares al lado opuesto de dicho vértice, o a su prolongación.

Las tres alturas de un triángulo se cortan en un punto llamado ortocentro, H.

 

Recta de Euler

La recta de Euler de un triángulo es una recta en la que están situados el ortocentro, el circuncentro y el baricentro de un triángulo (hay otros puntos notables del triángulo que no hemos visto que también se encuentran en esta recta).

Se denomina así en honor al matemático suizo, Leonhard Euler, quien demostró la colinealidad de los mencionados puntos notables de un triángulo, en 1765.

 

Se cumple que la distancia del baricentro al circuncentro es la mitad de la distancia del baricentro al ortocentro.  

Haga Click Aquí para ver ejemplos resueltos sobre las lineas notables y tomar apuntes en sus cuadernos:

 Haga Click Aquí para ver un video sobre propiedades de un triangulo 

Congruencia de Triángulos

Definición: Dos o más triángulos se dice que son congruentes si tienen la misma forma y el mismo tamaño.

Si dos triángulos son congruentes entonces los lados correspondientes son iguales y los ángulos correspondientes son iguales.  En geometría a los lados correspondientes se les suele llamar lados homólogos y a los ángulos correspondientes se les dice ángulos homólogos.

 

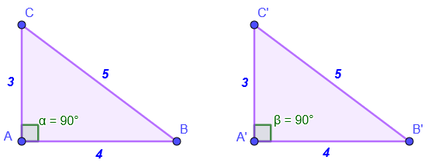
Los triángulos ABC y A’B’C’ son congruentes porque sus lados y ángulos correspondientes son iguales.

La expresión «El triángulo ABC es congruente al triángulo A’B’C’» se escribe así:

 

$$\Delta ABC\cong \Delta A^{\prime }{B}^{\prime }{C}^{\prime }$$

Teoremas de congruencia de triángulos
Teorema 1 (L-L-L)

Dos triángulos son congruentes si tienen sus lados correspondientes iguales. 

 

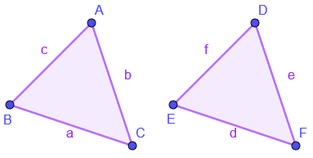
Dos triángulos son congruentes si tienen sus lados correspondientes iguales.

 

$$\begin{array}{cc}\stackrel{}{AB}& \cong \stackrel{}{DE}\\ \stackrel{}{}\end{array}$$

$$\begin{array}{cc}{BC}^{}& \cong \stackrel{}{EF}\\ \stackrel{}{}\end{array}$$

$$\begin{array}{cc}{\mathrm{CA}}^{}& \cong \stackrel{}{DF}\\ \end{array}$$

$$\begin{array}{cc}\therefore \Delta ABC& \cong \Delta DEF\end{array}$$

 

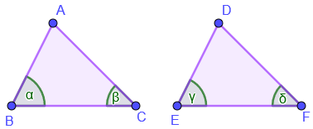
Teorema 2 (A-L-A)

  Dos triángulos son congruentes si tienen dos ángulos correspondientes iguales y el lado común adyacente a ellos también es igual. 

$$\begin{array}{cc}{BC}^{}& \cong \stackrel{}{EF}\\ \end{array}$$

$$\begin{array}{cc}\angle \beta & \cong \angle \delta \\ \end{array}$$

$$\begin{array}{cc}\therefore \Delta ABC& \cong \Delta DEF\end{array}$$

 

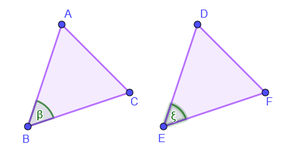
Teorema 3 (L-A-L)

 Dos triángulos son congruentes si dos lados correspondientes y el ángulo comprendido entre ellos son iguales.

 

 

$$\begin{array}{cc}\stackrel{}{AB}& \cong \stackrel{}{DE}\\ \end{array}$$

$$\begin{array}{cc}\angle \beta & \cong \angle \epsilon \\ \stackrel{}{}\end{array}$$

$$\begin{array}{cc}{BC}^{}& \cong \stackrel{}{EF}\end{array}$$

$$\begin{array}{c}{}^{}\\ \therefore \Delta ABC& \cong \Delta DEF\end{array}$$

 

 

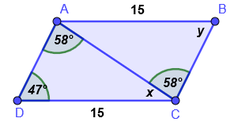
Ejemplo 1.

 En la figura AB es paralela a DC.  Determine si los triángulos son congruentes y cuales son los valores de los ángulos x, y. 

 

 Solución:  ­ ­

  Afirmaciones                     Justificacions

$$\begin{array}{cc}{AB}^{}& \cong {D\mathrm{C\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; Datos}}^{}\end{array}$$

$$\begin{array}{cc}\angle & \cong \angle \\ {}^{}\end{array}$$

 $$\begin{array}{cc}{A}^{}& \cong {\mathrm{CA\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; Datos\; Lado\; Común}}^{}\end{array}$$

$$\begin{array}{c}\mathrm{\angle y=\; 47°}\end{array}$$$$\begin{array}{c}\mathrm{Por\; ser\; Homólogo\; al\; ángulo\; ADC}\end{array}$$

 $$\begin{array}{c}\mathrm{\angle x=75° \; La\; suma\; de\; los\; ángulos\; internos\; del\; triángulo}\end{array}$$

$$\begin{array}{c}\mathrm{\angle CAB=\; 75° \; Alternos\; internos\; entre\; paralelas}\end{array}$$

$$\begin{array}{c}\mathrm{\Delta ADC\cong \; \Delta CBA\; \; \; \; \; \; \; \; \; Teorema\; A-L-A}\end{array}$$

  

Ejemplo 2.

 En la figura AB es bisectriz del ángulo CAD, AC es congruente al segmento AD. Demuestre que AB también es bisectriz del ángulo CBD. 

 

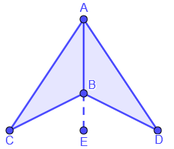
Solución:

  Afirmaciones                     Justificaciones

  $$\begin{array}{cc}\angle & \cong \angle \end{array}$$$$\begin{array}{c}\angle \end{array}$$

$$\begin{array}{cc}{A}^{}& \cong {\mathrm{AD\; \; Datos}}^{}\end{array}$$

 $$\begin{array}{cc}{A}^{}& \cong {\mathrm{BA\; \; Datos\; (por\; ser\; lado\; común)}}^{}\end{array}$$

$$\begin{array}{c}\mathrm{\Delta ABC\cong \; \Delta ABD\; \; \; \; \; \; \; \; \; Teorema\; L-A-L}\end{array}$$

$$\begin{array}{cc}\angle & \cong \angle \end{array}$$

 

$$\begin{array}{cc}\angle & \cong \angle \end{array}$$$$\begin{array}{c}\angle \end{array}$$$$\begin{array}{c}\angle \end{array}$$$$\begin{array}{c}\angle \end{array}$$$$\begin{array}{c}\angle \end{array}$$

Por lo tanto, el segmento AE biseca al ángulo CBD

 Ejercicios:

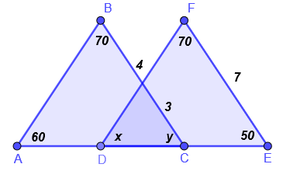
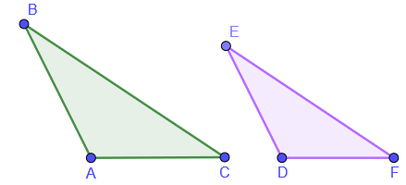
 1. Determine el valor de x, y. Justifique si existe congruencia. 

 

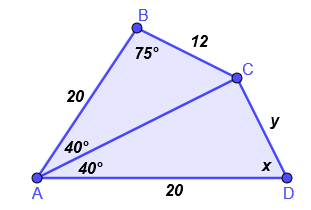
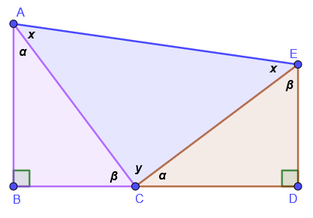
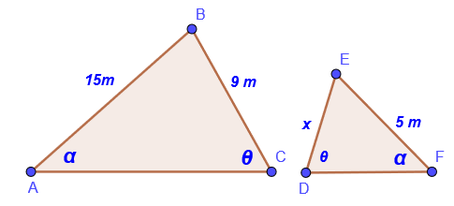
2.  Determine el valor de x, y. Justifique si existe congruencia.

 

 

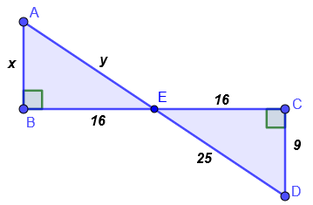
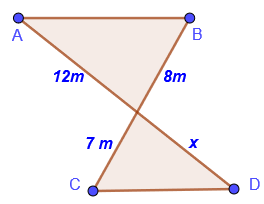
3. Calcular los valores desconocidos. Justifique si existe congruencia entre triángulos.  Considere que además se cumple que;

CD es bisectriz del ángulo ECB.

$$\begin{array}{cc}\angle z& =25°\\ {}^{}\end{array}$$

$$\begin{array}{cc}{CE}^{}& \perp {AD}^{}\end{array}$$

$$\begin{array}{c}{\mathrm{4.\; Determinar\; el\; criterio\; de\; congruencia\; entre\; triángulos\; y\; calcular\; los\; valores\; desconocidos.}}^{}\end{array}$$

5. Calcule el valor del ángulo x. Indique si existe al menos un par de triángulos congruentes. Considere que:

$$\begin{array}{cc}\stackrel{}{AB}& \cong \stackrel{}{CD}\end{array}$$

$$\begin{array}{c}{}^{}\\ \stackrel{}{BC}& \cong \stackrel{}{DE}\end{array}$$

Semejanza de Triángulos

 Dos triángulos se dicen ser semejantes si tienen la misma forma, aunque no necesariamente igual tamaño.  Los lados homólogos de dos triángulos semejantes son aquellos que son adyacentes a cada uno de los ángulos congruentes, es decir son los lados correspondientes

 

$$\begin{array}{c}{\mathrm{Los\; lados\; homólogos\; de\; los\; triángulos\; de\; la\; figura\; son:\; a\; y\; f,\; c\; y\; d\; y\; b\; y\; e\; respectivamente.\; Los\; ángulos\; homólogos\; son:\; <B\; y\; <E,\; <A\; y\; <F\; y\; <C\; y\; <D\; respectivamente.\; Simbólicamente\; en\; matemáticas\; indicamos\; de\; la\; siguiente\; manera\; que\; dos\; triángulos\; son\; semejantes:}}^{}\end{array}$$

 Propiedades fundamentales
1.  Dos triángulos son semejantes si sus ángulos correspondientes son iguales:

$$\begin{array}{cc}\angle A& =\angle F\end{array}$$

$$\begin{array}{c}\\ \angle B& =\angle E\\ \end{array}$$

$$\begin{array}{cc}\angle C& =\angle D\end{array}$$

2. Dos triángulos son semejantes si la razón de sus lados correspondientes es constante.  Dicho de otra forma, sus lados correspondientes son respectivamente proporcionales.  

AB / FE = BC / ED =AC / FD

Ejemplos:
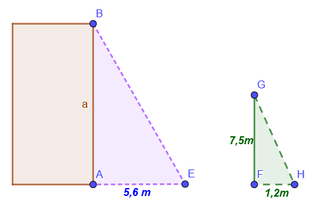
1. Calcular la altura de un edificio que proyecta una sombra de 5,6 m en el mismo instante que un poste de 7,5m proyecta una sombra de 1,2 m.

$$\begin{array}{cc}\Delta ABE& \sim \Delta FGH\end{array}$$

$$\begin{array}{c}\mathrm{AB\; /\; FG\; =\; AE\; /\; FH}\end{array}$$

$$\begin{array}{c}\mathrm{a\; /\; 7.5\; =5.6\; /\; 1.2}\end{array}$$

$$\begin{array}{c}\mathrm{de\; donde\; a\; =\; 35\; cm}\end{array}$$

$$\begin{array}{c}\mathrm{Teoremas\; de\; semejanza\; Teorema\; 1.\; Dos\; triángulos\; son\; semejantes\; si\; tienen\; dos\; pares\; de\; ángulos\; homólogos.}\end{array}$$

$$Si\angle A=\angle Dy\angle C=\angle E\Rightarrow \Delta ABC\sim \Delta DFC$$

$$\mathrm{Teorema\; 2.\; Dos\; triángulos\; son\; semejantes\; si\; tienen\; un\; par\; de\; ángulos\; homólogos,\; y\; los\; lados\; correspondientes\; que\; incluyen\; cada\; ángulo\; son\; proporcionales.}$$

$$\mathrm{Si \angle B\cong \angle E}$$

$$\mathrm{Teorema\; 3.\; Dos\; triángulos\; son\; semejantes\; si\; los\; tres\; pares\; de\; lados\; correspondientes\; son\; proporcionales.}$$

$$\mathrm{Si\; AB\; /\; DE\; =\; AC\; /\; DF\; =BC\; /\; EF}$$$$\mathrm{\Rightarrow \Delta ABC\sim \Delta DEF}$$

$$\mathrm{Ejemplo}$$

$$\mathrm{Determine\; si\; los\; triángulos\; de\; la\; imagen\; son\; semejantes\; (justifique\; su\; respuesta).\; Si\; hay\; semejanza\; determinar\; el\; valor\; de\; x.}$$

$$\mathrm{Los\; triángulos\; son\; semejantes\; ya\; que\; tienen\; dos\; ángulos\; homólogos,\; además\; los\; lados\; opuestos\; al\; ángulo\; ϴ\; (correspondientes)\; son\; proporcionales.\; AB\; es\; proporcional\; a\; EF\; porque\; se\; oponen\; a ϴ\; y\; BC\; es\; correspondiente\; a\; DE\; por\; oponerse\; al\; ángulo \alpha }$$

$$\mathrm{AB\; /\; EF\; =\; BC\; /\; DE}$$

$$\mathrm{15\; /\; 5\; =\; 9\; /\; x}$$

$$\mathrm{x\; =\; 45\; /\; 15}$$

$$\mathrm{x\; =\; 3}$$

$$\mathrm{R./\; El\; valor\; del\; lado\; DE\; es\; 3m.}$$

$$\mathrm{Ejercicios}$$

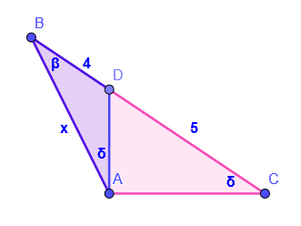
1. En la figura, calcular el valor de AB. 

 

2. El poste de un semáforo peatonal de 2m de altura proyecta una sombra, a la misma hora en que un edificio proyecta una sombra de 80 m.  Hallar la altura del edificio. 

3. Los lados de un triángulo miden 24 m., 18m. y 36 m., respectivamente. Si los lados de otro triángulo miden 12m., 16 m. y 24 m., respectivamente. Determina si son o no semejantes, justificando tu respuesta.  

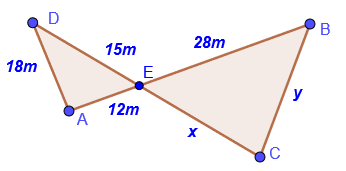
4. Con los datos de la figura, obtener los valores de los lados EC y BC. 

 

$$\mathrm{5. En\; la\; figura\; AB\; y\; CD\; son\; paralelas. \; Determine\; el\; valor\; de\; x.}$$

$$\mathrm{Triángulo\; Isósceles}$$

$$\mathrm{Un\; triángulo\; es\; isósceles\; si\; tiene\; dos\; lados\; iguales}$$

$$\mathrm{Propiedades}$$$$\mathrm{Para\; demostrar\; varias\; propiedades\; del\; triángulo\; isósceles,\; trazaremos\; la\; bisectriz\; del\; ángulo\; opuesto\; a\; la\; base.}$$$$Analicemos los triángulos ACO y BCO.El ángulo ACO es igual al ángulo BCO, dado que la recta CO es bisectriz.El lado AC es igual al lado BC, dado que son los lados iguales del triángulo isósceles.El segmento CO es igual al segmento CO.Observando las tres afirmaciones anteriores y considerando el criterio de congruencia LAL, podemos asegurar que los triángulos ACO y BCO son iguales, entonces: Los ángulos en los vértices A y B son iguales.Los segmentos AO y OB son iguales.Los ángulos AOC y BOC son iguales y como son adyacentes son rectos.Por lo tanto llegamos a las siguientes conclusiones:En todo triángulo isósceles:Los ángulos opuestos a los lados iguales, son iguales.La bisectriz del ángulo opuesto a la base, corta a la base en su punto medio. La bisectriz coincide con la mediana del lado AB.La bisectriz del ángulo opuesto a la base, es perpendicular a la base. La bisectriz coincide con la altura correspondiente al lado AB.Triangulo Equilátero Un triangulo equilátero es aquel quee tiene los tres lados de igual longitud.Observe cómo es un triángulo equilátero.  Características de un Triangulo EquiláteroTe mostramos las principales características del triángulo equilátero.Sus tres lados son iguales.Sus ángulos internos son iguales a 60°.Las Líneas Notables:  Mediatriz, Bisectriz, Altura y Mediana son congruentes.Los Puntos Notables: Circuncentro, Incentro, Ortocentro y Baricentro coinciden en el mismo punto.La Recta de Euler del Triángulo Equilátero es un punto.El Centro del Triángulo Equilátero (centro de gravedad) es el centro de la Circunferencia Inscrita y Circunscrita a él.El triángulo equilátero tiene tres ejes de simetría.$$

$$PropiedadesExisten diversas propiedades del triángulo equilátero. Trataremos a continuación los teoremas más importantes y que nos ayudarán en la resolución de problemas.Propiedad N° 01:En un triángulo equilátero las líneas notables: Mediana, Bisectriz, Altura y Mediatriz son iguales en segmento y longitud. Véase la Figura: 01. Propiedad N° 02:Al trazarse cualquier línea notable: bisectriz, altura, mediana y mediatriz en un triángulo equilátero, estas dividen al triángulo equilátero en dos triángulos rectángulos congruentes (véase Figura: 02). Propiedad N° 03:En un triángulo equilátero los puntos notables: baricentro, incentro, circuncentro y ortocentro coinciden en un mismo «punto» y se cumple que la distancia de dicho punto a un vértice es el doble de su distancia a la base. Véase la figura 04: Observación:Es importante conocer lo que se cumple en la figura 05: Si en la figura dada cumple que:AB = BC; ym∠B = 60°Entonces, al trazar AC, se forma el triángulo equilátero ABC.Esto se puede considerar como un principio de cómo dibujar un triángulo equilátero.Haga Click Aquí para ver un video con ejercicios sobre triángulos isósceles y equilátero  Click Aquí para la práctica 1Click Aquí para la práctica 2 Click Aquí para la práctica 3$$

$$n$$